Nuclear Fusion Part 1: Theory

Two basic forms of nuclear reactions have been identified by physicists: nuclear fission, which we are all surely somewhat familiar with (even if we don't know it), and nuclear fusion, her less understood sister. Between 6th and 8th grade, I constructed a small nuclear fusion device. On this page, I've detailed the theory and construction of the device, to provide readers with some background. A thorough understanding of some not-so-complicated physics is essential for understanding the principles of fusion, the reaction that produced the atoms in your body and everything else around you. So let's get to the basics!

Fusor

Part 1 of Part 1: Plasma

In normal, everyday life, we're pretty familiar with the states of matter. Your laptop is a solid, your coffee is a liquid, and the air you're breathing is a gas. But the fourth state of matter is much less well known (although it's pretty common). Plasma is the high energy form of a gas and the form of matter in which fusion occurs (some common plasmas: welding arcs, lightning, plasma tv cells, the sun and other stars, and fire can be considered a very weak plasma).

Now we just talked about energy, but what really is energy? Where does it come from? Physics is a lot of names that you put together to make more names. The most basic quantities in physics are mass (amount of matter inside of something), distance/length, and time (There are some others, see below). You can come up with most other quantities just from these: speed (distance over time), velocity (speed with direction), acceleration (velocity over time), and force (mass times acceleration).

Forces are the next step to understanding energy, and therefore understanding plasma. Forces are acting on us all the time: the force of gravity, pulling you down, the force of the ground, pushing you up, and the force of friction, stopping your car. The next quantity we can derive is work, the force times the distance over which it is applied, and from there we get to energy, a measure of the amount of work done/the capacity to do work. In the image below, the cosine just means that the direction the object moves has to be the same direction the force is applied for work to be done.

The two most basic kinds of energy are kinetic and potential. Kinetic is energy in motion (think about a car driving down a highway), and potential is the energy of position (think about a ball at the top of a hill). So a plasma has what kind of energy? The kinetic energy of the particles making it up (the name for the average kinetic energy of all of the particles should be pretty familiar: temperature).

So this plasma has particles moving around really fast, but so do gases, so why is it different? This has to do with the atomic structure. Electrons orbit the nucleus of the atom at (roughly) set distances depending on the amount of energy they have, the higher the energy, the farther out they move. In a plasma, the individual atoms and the electrons in these atoms have received so much energy that their electrons aren't even bound in their orbits around the nucleus anymore, so it's just a really hot slush of electrons and nuclei. This is still a bit simplified though; not all of the electrons may have been liberated, so the atoms might, instead of having no electrons, have less than normal, meaning that they are ions, not just nuclei. The images below show the difference between gas and plasma (black = gas atoms or molecules, red = ions, blue = electrons. Not to scale at all.)

From this arises another form of energy: electric potential. The nuclei (or ions), dense positive charges, are completely (or partially) exposed and moving really fast. So now, like opposite poles of a magnet, these individual nuclei repel each other whenever they get close. So our final definition of plasma (which is still pretty simplified) is: a super-heated gas made into a soup of nuclei/ ions and electrons that are moving really fast, and the nuclei repel each other. So if the nuclei repel each other, and if we need to get them close together to fuse, HOW DOES FUSION HAPPEN???

Part 2 of Part 1: Fusion

Now it's time to get to the more interesting stuff. Armed with a rough understanding of plasma, we can begin to see a vague idea of fusion reactions. We've got a bunch of nuclei, and we need to get them to fuse. The problem we're finding is that they're all positively charged, so they repel each other. This brings up another good question. If the nuclei of atoms are made up of positive protons and neutral neutrons, how do the protons stay together? They're all positive, so by logic they should fly apart. The answer is the strong nuclear force.

Physicists have isolated four fundamental forces of nature: gravity, electromagnetism, strong nuclear force, and weak nuclear force. Gravity and electromagnetism (electricity and magnetism) are pretty well known and understood, but the other two are less so. Gravity is the attraction between masses. Electromagnetism is the attraction and repulsion of positive and negative charges. The weak force is responsible for forms of radioactive decay, and the strong force holds nuclei together.

So far, all of the forces we observe can be traced back down to these four forces, in fact, one of the biggest quests of modern physics is to find a grand unifying theory or GUT to reconcile the four into one working description of the universe. The forces we're interested in to begin with are the electromagnetic and strong forces.

(A fun take on the bosons, or force carrying particles, of the fundamental forces.)

The electromagnetic force is causing the repulsion (positive charge repels positive charge, via Coulomb's Law. See below). The strong force is joining the repulsive nuclei. Both forces are mediated by force-carrying particles called bosons. The E/M force is mediated by photons and has an infinite range. The strong force is mediated by gluons and has a range of 0.000000000000001 meters (10^-15 meters). The strong force may be extremely strong (137 times stronger than E/M), but the dilemma is bringing the nuclei so close together that the strong force can take over.

(Past that barrier, the strong nuclear force takes over, but up until that point, the E/M force is repelling, so the nucleon needs a lot of energy.)

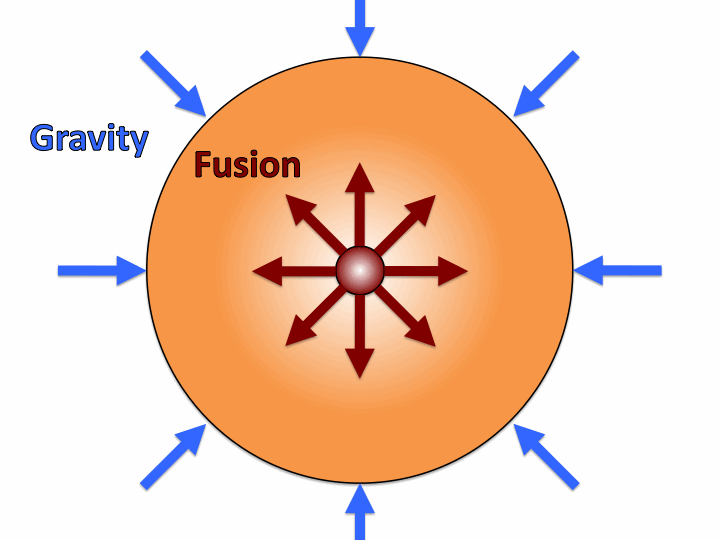
The best way to address this problem is by examining how fusion happens in the sun. The sun began as a large cloud of hydrogen gas. By large, I mean 1.3 million times the volume of Earth and 333 thousand times the mass. With such large masses, the force of gravity is extremely strong. The large mass becomes compacted into a ball because of the gravitational attraction of all of the hydrogen. The force of gravity is so strong, that the pressure and temperature become immense in the center due to all of the mass pressing in on the core. With so much energy being supplied from the heat, the gas becomes ionized (a plasma). Then, with the immense pressure, nuclei are pressed close enough together for the strong force to take over, and fusion occurs.

In the sun, the immense force of gravity pulling an extremely large mass together drives the reaction, providing the perfect conditions for fusion. That seems pretty hard to replicate on Earth. But before we get into replicating the reaction, there are a couple more advanced things I want to take a look at. First off: how does fusion produce energy?

Part 3 of Part 1: Quantum

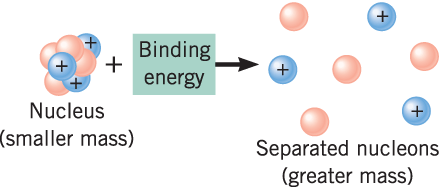
Right now, it seems like fusion takes a ton of energy, but we're not really seeing how any energy would be released. The answer actually comes from chemistry. It's called binding energy. Binding energy is the energy that is released to stabilize the nucleus. It's the energy that holds the nucleus together.

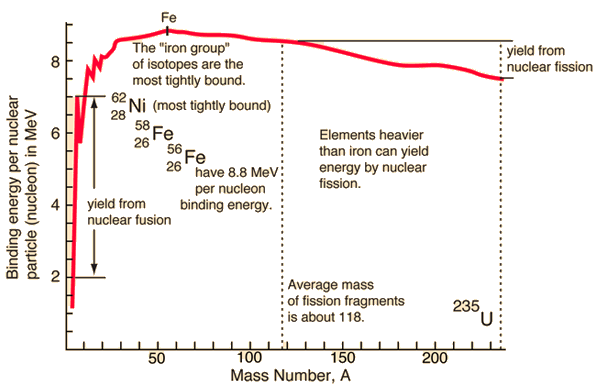
On the periodic table, the light elements have low binding energies because they don't have that many protons to hold together. And the heavy elements have lower binding energies too because they have so many protons that they're very unstable (most of them are radioactive to try to remedy this instability). The middle ground though has elements with higher binding energies. So, if you take two small, low binding energy atoms and fuse them, then the resulting nucleus will have a higher binding energy.

This higher binding energy will be released to stabilize the new nucleus, and that energy is the product of fusion that we're interested in. Nuclear fission, the inverse, occurs by splitting a heavy nucleus into two or more higher binding energy products. The energy, in either case, is a product of the famous E=mc . Part of the mass of the nucleus is converted into binding energy, which is released as kinetic energy of the products and possibly light/other electromagnetic radiation, like gamma rays.

The final step to understanding the theory behind fusion is the realm of quantum mechanics. There are two basic principles in quantum mechanics. Basically, the idea is that physics at the subatomic, or quantum level is different in behavior than the macroscopic world and cannot be explained by our classical notion of physics. Instead of concrete laws, the two main principles are based around probabilities: particle-wave duality and the uncertainty principle.

Particle-wave duality defines subatomic particles as behaving as both particles and waves, not one or the other (subatomic particles exhibit properties of both). The uncertainty principle states that you can't know both the position and momentum of a particle certainly (if you know one with certainty, the other is very uncertain).

Particle-wave duality arises from actual observations of the properties of subatomic particles. The uncertainty principle arises from something called conjugate variables. This can best be understood from considering the example of time and frequency of a musical note. Let's say you're playing the flute and you play a note and hold it out for a while. That produces a sound wave that looks something like this:

Now, this wave has a pretty well-defined frequency, but what would you say if I asked at what point in time does this wave occur? Clearly, it doesn't have a well-defined location in time. But what if you play a super short note, like a nearly infinitely short note? Let's say we zoom in a lot and it looks something like this:

Now we have a well-defined location in time, but the note is so short that it doesn't really have a well-defined concept of frequency. An early statement of quantum mechanics was that position and momentum are conjugate variables, like time and frequency in the example, lending an inherent, probabilistic nature to subatomic particles.

Now let's apply this to fusion. Let's imagine that our nuclei are made of paint on a canvas. Rather than being dots, like we would expect, they're more like streaks, and the thicker areas of the streaks are where the nucleus most probably is. Now we'll make the repulsive electromagnetic barrier (the Coulomb Barrier) a wall. If the nucleus was ball like, it would hit the wall and bounce back. But let's say it's like our canvas streak. The streak comes at the wall, and we'd expect it to stop and bounce back, but what if one of those thinner areas on the end makes it through the wall. Maybe it's so thin, that it was just able to pass through. This means that the tiny piece that passed through represents a tiny probability that the nucleus passes through the repulsive Coulomb barrier and fuses.

This example is to bring light to the reality: many nuclei that participate in fusion reactions don't have sufficient energy to do so. What actually happens is that due to their probabilistic nature, they are able to "tunnel" through the electromagnetic barrier, and the strong force takes over.

This was a pretty intense look at the theory. Now we're gonna look at how a fusion reaction is made on Earth.

Nuclear Fusion Part 2: Fusor

Alright, the theory wasn't so bad. Now we have a pretty good idea of what to do, but how do we go about doing it? This next section is going to look into the practical concepts. I've detailed the construction of my device, and some other designs.

Part 0 of Part 2: The History

The history of practical fusion starts with the proposition of fusion reactions in stars, after Einstein's groundbreaking publications on relativity. British astrophysicist Arthur Eddington suggested that stars produce energy turning hydrogen into helium in his 1926 paper, Internal Constitution of the Stars (further work on nucleosynthesis in stars was done by Hans Bethe, who won a Nobel Prize for his work). Using particle accelerators (see my particle accelerator page for more info about accelerators) designed by John D. Cockroft and Ernest T.S. Walton (early pioneers of particle physics research) Ernest Rutherford (widely considered the father of nuclear physics, having discovered the proton/nucleus, and theorized the existence of the neutron) performed early fusion experiments in the thirties, shooting protons at a deuterium target, and creating deuterium to helium fusion reactions. His assistant, Mark Oliphant, further developed early fusion reactions, discovering tritium (the third isotope of hydrogen, consisting of a proton and two neutrons) and helium-3 (an isotope of helium), demonstrating the fusion of heavy-hydrogens. Accelerator fusion devices produced reactions, but on a very small scale. With the rise of fission devices (particularly nuclear weapons), physicists like Enrico Fermi explored the idea of fission-driven fusion reactions (theoretically). Intrigued by Fermi's ideas, Edward Teller tried to apply them experimentally, succeeding with the creation of a thermonuclear weapon design in the early fifties, which would be used extensively to develop new weapons. Meanwhile, other researchers, chiefly in the Soviet Union and the U.S.A. explored practical fusion reactions for an energy source.

The Methods

Fusion promised to be the Holy Grail: nearly four million times as much energy as an equal mass of coal, oil, or gas, and four times as much energy as equal mass fission reactions, extremely abundant fuel (deuterium and hydrogen from water), and environmentally friendly products (inert helium, opposed to pollutant gases from coal and radioactive waste from fission). Two main ideas for how to produce fusion emerged: magnetic confinement and inertial confinement. Most research was concentrated on magnetic confinement, confining the plasma in a chamber with a magnetic field, which also provides the energy to heat the nuclei to fusion temperatures.

The Stellarator

During the '50s and '60s, the stellarator design, proposed by Lyman Spitzer, dominated the fusion research scene. To learn more about the stellarator you can watch this great video: https://www.youtube.com/watch?v=vqmoFzbZYEM . It's making a comeback recently due to modern computing technology and construction techniques (Take a look at this: https://www.popularmechanics.com/science/energy/a21945982/german-nuclear-fusion-experiment-sets-records-for-stellarator-reactor/ ). But in the '50s, the practical design resulted in many instabilities, and so it took a backseat to the more promising and practical tokomak from Russia.

The Tokomak

Basically, the idea comes from a solenoid. If you wrap a wire in a cylindrical coil, it creates a uniform magnetic field when you run a current in it, and this device is known as a solenoid. If you take a gas and put it in a strong enough solenoid, the gas can become ionized and possibly hot enough to fuse. The only problem is that the magnetic field accelerates the plasma along the axis of the cylinder. So in order to keep the plasma inside of our solenoid, it would have to be infinitely long. Instead, what if we wrap the cylinder around into a donut shape, or torus, and use this as our fusion vessel. Then you keep it going for a long time. This is the principal idea of a tokomak. (Also look at the pictures). There are instabilities in the plasma with this device as well because, on the inside of the torus, the field is stronger because the magnets are closer to each other. The plasma instabilities can be paralleled to squishing a balloon; however you squish it, the air finds new ways to keep poking out (this is a pretty simplified view). Some of today's most promising fusion research is in tokomaks (Check out ITER: https://www.iter.org/).

Inertial Confinement

Inertial confinement fusion uses short pulses of immense energy to induce fusion reactions, creating an area of high pressure and density in the target. Often, this method uses powerful lasers aimed at a hohlraum, which is induced to produce x-rays by heating, which strike a tiny deuterium or deuterium/tritium target, causing it to compress.. To learn more about this check out NIF: https://lasers.llnl.gov/science/icf. That's an overview of the major points of fusion research. Now onto my device.

These are some images related to NIF, the National Ignition Facility, at Lawrence Livermore National Lab. The top image details the general process, the middle left explains the hohlraum, the middle right is an image of the actual hohlraum, and the bottom left is a picture of part of the NIF facility.

Inertial Electrostatic Confinement

Growing up in southwestern Utah, Philo T. Farnsworth was far removed from the booming centers of scientific research in America, big cities like Chicago and New York. Intrigued by Popular Science and the inventions of his day (like the telephone and gramophone), in 1922, he presented the theory that would become the basis for the electronic television to his chemistry teacher, at the age of 15. 5 years later, he constructed the first all-electronic television and presented it in San Francisco. From his invention, and with help from his friends, Farnsworth funded his future invention pursuits. During WWII, he developed the basis for radar, blacklight, and an IR telescope. Some more of his inventions include the cold cathode ray tube, air traffic control system, gastroscope, and the electron microscope. By his death, he held over 300 U.S. and international patents. He's relevant to fusion research because, in the'50s, he too was interested in the prospects of fusion power. In 1965, he patented the "fusor," which operates on the principle of inertial electrostatic confinement. Basically, we take our deuterium and possibly tritium gas and put it in a container with an electrode at the center. Then, we put a very high electric potential on it (high voltage), with the negative region in the center of our vessel. The electrons are ripped off the nuclei and go to the outer positive shell. The positive nuclei are attracted to the negative core and accelerate towards it. Now they should hit the negative electrode, but what if we make our electrode like a shell? Then some of the nuclei may be moving so fast that they don't hit the electrode and go into the center. If our shell is spherical, nuclei from all sides come towards the center, and the few that are moving fast enough to move past the shell could get close enough to fuse. It is "inertial," because we rely on their inertia or tendency to stay moving in a straight line, "electrostatic" because we use an electric field to provide the acceleration, and "confinement" because we are confining them to the center of our vessel. Today, there is actually an online community of amateur fusion researchers, inspired by Farnsworth's design. Check it out: www.fusor.net . The type of device I constructed was a Farnsworth fusor, mostly for educational and recreational purposes, rather than research. The fusor has been mostly ruled out as a viable energy source, but it does find a lot of other uses, which I'll discuss later. Now onto actual construction plans/methods.

Part 1 of Part 2: Vacuum

Creating an IEC fusion device requires establishing a vacuum, or a region with very few air molecules (and hence, very low pressure). There are two reasons for this. Primarily, we must remove the air from our reaction vessel because our fuel is deuterium, not air, so we need to get rid of it so we are not creating an air plasma, which will not produce the fusion reactions we are interested in (for reference, air is about 21% oxygen, 78% nitrogen, and 1% argon, with small traces of other gases, like carbon dioxide at 0.04%).

An air plasma will produce fusion reactions of deuterium, but very few because deuterium makes up an extremely small percentage of the composition of the air. For an idea of scale, hydrogen gas makes up 0.000053% of the air, and deuterium is about 0.0156% of that (there are also other hydrogen compounds like water vapor, but I've disregarded them just to illustrate a point). There will also possibly be very very very few other types of fusion reactions (such as fusion of carbon), but the probability of these occurring is extremely low because of the immense energy required (carbon is about six times as massive as deuterium, meaning it requires a lot of energy to accelerate, and twelve times as positively charged, meaning carbon nuclei repel each other a lot more).

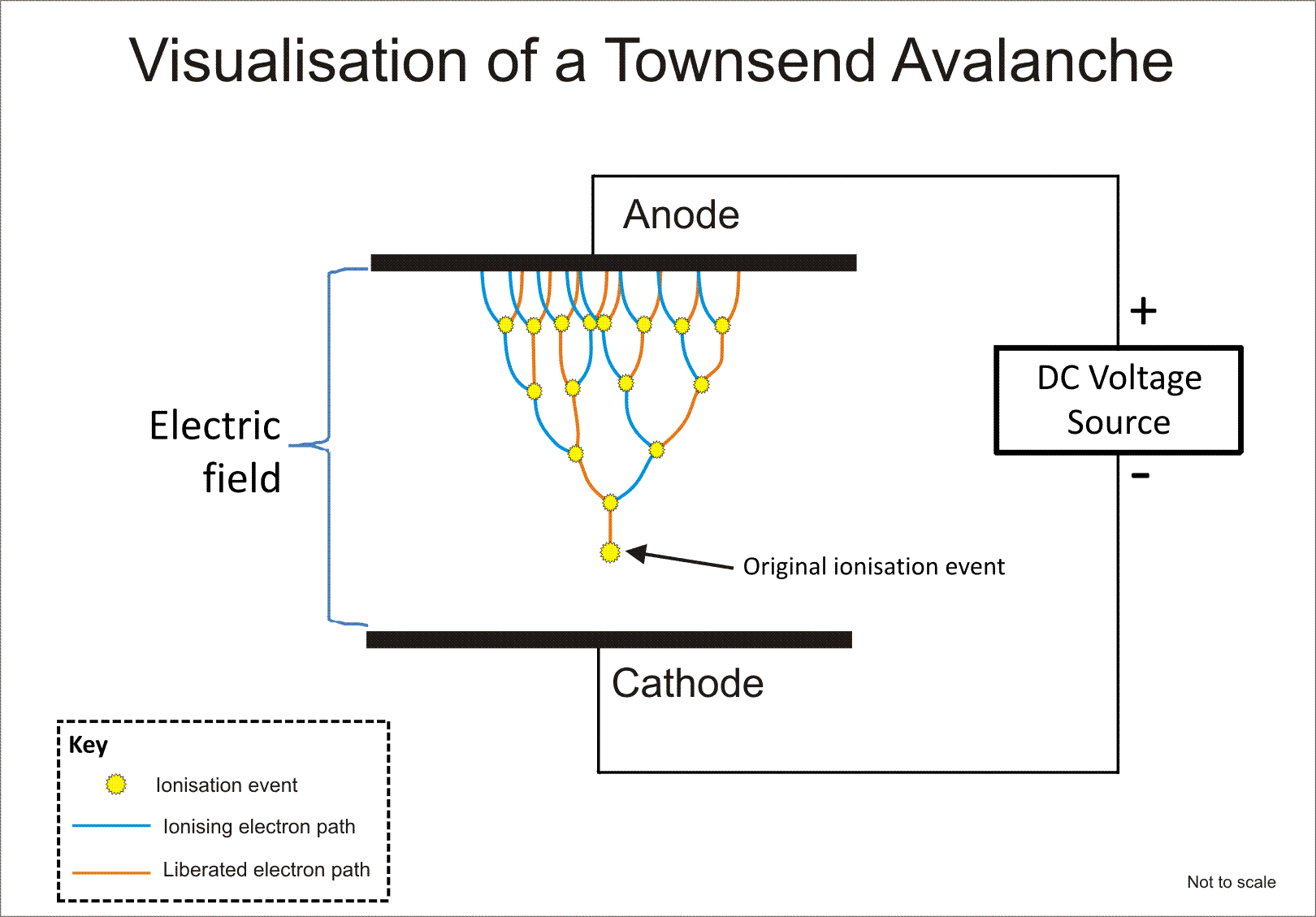
The second reason for creating a vacuum is to reduce the amount of energy required to generate the plasma. The more molecules present, the more difficult it is to ionize all of them. Instead of having to provide, let's say five molecules of gas with ionization energy, if we must provide 500, then the total energy input increases drastically. This is expressed in a relationship known as Paschen's curve, which I've included an image of below. As electrons are ripped off of atoms in a strong electric field, they accelerate towards the positive terminal, hitting other atoms/molecules along the way, and causing more electrons to be released, and hence more atoms/molecules to be ionized. This can cause a cascade, electron avalanche, or Townsend discharge, where one electron may knock two off the next atom, and those two knock off two more, resulting in an exponential increase in ionization.

If the pressure is high, the molecules/atoms are very close together, so the electron doesn't get much distance between atoms/molecules to accelerate, and doesn't hit them with much energy, thus resulting in less electrons being knocked off and less ionization. But if we decrease the pressure, the larger distances provide better acceleration. However, if we decrease the pressure too much, it becomes difficult to form a plasma because the distances are so far that an electron might not hit anything on its way to the cathode. So less atoms/molecules will be ionized. Hence, the best pressure for creating a fusion plasma is very low, but not extremely low (rough vs. high/ultra high vacuum). I'll provide some numbers for this later.

Thus, the vacuum system is necessary to remove the air from the system before filling it with deuterium, and it is necessary to maintain a low pressure of that deuterium in order to provide optimal fusion circumstances.

The first step to creating a vacuum system is finding a device to generate the vacuum. Such a device is known as a vacuum pump, Vacuum pumps used in fusion research come in many varieties, including but not limited to rotary vane, scroll, turbo-molecular, oil diffusion, and ion pumps. I won't discuss the actual operating principle of these pumps, as that is a whole study of its own. If you're interested, check out Pfeiffer Vacuum and explore the Know-How section.

In general, a vacuum system for a vacuum-requiring piece of equipment requires two pumps: a roughing pump and a higher vacuum pump. The roughing pump is the workhorse, it pulls out most of the air and gets the system to the "rough" vacuum range (from 50-1 millitorr, or about one 15,000th to one 760,000th of atmosphere. Atmosphere is 760 torr). Then the high vacuum pump increases the vacuuming "power" of the roughing pump, allowing the system to reach even lower pressures, in the high vacuum range (one 100th to one 100,000th of a millitorr) and potentially the ultra high vacuum range (lower than about one 1,000,000th of a millitorr). For my system, through much eBay scrounging, contacting companies, and requesting student discounts, I acquired a Fisher Scientific dual-stage rotary vane pump as my roughing pump, and a Varian VHS-4 diffusion pump, a system capable of reaching one 250,000th of a millitorr.

Next, some means of measuring the vacuum generated by the pumps is necessary. This device is referred to as a vacuum gauge. There are many different types for the different ranges: Bourdon/dial, piezo, diaphragm, capacitance manometers, pirani, thermocouple, cold cathode ion, hot cathode ion, and more. For more info, I would once again recommend looking at Pfeiffer Vacuum's Know-How page. Also, this is a good guide, from University of Notre Dame. Generally, similar to the pumps, you need a rough gauge and a high vacuum gauge for an optimal measurement system.

For my fusor, I was not prepared to invest in a full-fledged gauge system, and instead I relied on a thermistor gauge, which would more likely be employed in commercial HVAC services rather than lab applications. It only measured down to 1 millitorr. For the performance of the system below a millitorr, I had no reliable measurement.

The last part of the vacuum system is the chamber itself. The most common material is stainless steel, to prevent the release of carbon contaminants present in normal steel. Now, the chamber is usually designed spherically, to create a uniformly-directed field, aimed at the center, but it's not necessary. Next, the ports. The chamber needs to be vacuum sealed and provide ports for a few different things. The first port is for the power, supplied to the center grid. The second port is for the vacuum pumps, allowing them to evacuate the chamber. The third port is for a gas supply, providing the deuterium fuel. The fourth port is for a view port, allowing the plasma to be observed. A fifth port can also be added for the gauge, however the gauge can also be installed in the same line as the pumps. In a complete/more professional system, there would be separate gauges for monitoring pump performance and chamber pressure, with the chamber gauge on the fifth port.

These ports are welded to the chamber on one side, using a method known as TIG (More Info). The other side is flanged, with one of many types of flanges. A flange is a vacuum fitting used to connect two segments, designed such that it can be disconnected, unlike welds. In order to maintain the vacuum, however, some means of sealing must be devised. The simplest is compressing a rubber ring to fill any gaps and keep air from entering. Another, better method uses the compression of a copper ring instead of rubber. For more info on flange types, look at the UND link above.

Part 2 of Part 2: Power

Coming Soon!

Also, all image references coming soon.

Part 3 of Part 2: Neutrons

Coming Soon!